Me
Maosheng Yang
Ph.D. candidate
Intelligent Systems dept.,
TU Delft
email: m.yang-2@tudelft.nl

About

Hi! I am a coming Ph.D. graduate from TU Delft. I have been advised by Dr. Elvin Isufi and Prof. Geert Leus in the dept. of Intelligent Systems. I am also affiliated with Aidro Lab (TU Delft AI Lab Programme). Before my PhD, I did my master in Electrical Engineering (cum laude) in the Signal Processing Systems group of TU Delft, where I worked on graph signal processing with Dr. Mario Couriño for my thesis, and my PhD advisors. I did my bachelor in communication engineering in Beijing Jiaotong University.

I love picking up new things and tools, enjoy the opportunity of doing research, and strive to bring research into practice. During my PhD, I have developed machine learning models for flow-type data in networks such as information/money/water flows, ocean currents, etc. These models range from convolutions to neural networks, Gaussian processes, and generative models, and are aware of the flow physical properties, like flow conservation, arbitrage-free. I have applied them to filtering, regression, interpolation, and prediction in various real-world networks. I see a lack of network-based machine learning tools in practice and hope to bring them into practice.

Research Interests

  • Machine Learning for Networked Data
  • Generative Models
  • Optimal Transport, Stochastic Dynamics
  • Applications involved with data over networks

Education

TU Delft, Sep, 2020 - Aug, 2025
  • Ph.D. student (ongoing)
TU Delft, Sep, 2018 - Aug, 2020
  • M.Sc in Electrical Engineering (cum laude, 9.3/10.0)
Beijing Jiaotong University, Sep, 2014 - Jul, 2018
  • B.Sc in Telecommunication Engineering (93+/100)

News

  • My paper Topological Schrödinger Bridge Matching is accepted to ICLR Spotlight, 2025. [Paper]
  • I gave an invited talk on my PhD work at Applied Math Seminar in Utrecht University. [Slides]
  • I have been awarded a travel fund from G-research to attend the LOGML summer school in July. Appreciate the opportunity very much!
  • I gave an invited talk on my PhD work to Computational neuroEngineering Lab at the University of Florida. [Slides]
  • I gave an oral presentation at the DEEPK workshop in KU Leuven. [Slides]
  • I gave a talk on my work on Simplicial Convolution at AMLab, Amsterdam. [Slides]
  • Our paper on "Hodge-compositional Edge Gaussian Processes" was accepted by AISTATS 2024.
  • I gave a talk about my work on Simplicial Convolution at the Delft AI Energy Lab.

Research

This is a draft of my PhD thesis.

See a full list on my google scholar. Below are some selected research projects.

Topological Schrödinger Bridge Matching
Maosheng Yang (single-author)
ICLR Spotlight, 2025
[paper] [code] [slides]
  • Investigate how to match signal distributions over nodes and edges of a network by building the Schrödinger bridge (SB) problem, i.e., the dynamical optimal transport in graphs and simplicial 2-complexes.
  • Use topological stochastic dynamics such as, topological heat diffusion mixed with Brownian motion, as the reference process to guide the matching. For the case of two Gaussian processes, we looked for the optimal topological Schrödinger bridge, based on tools of Girsanov theorem, Doob's h-transform, etc..
  • Propose topological SB generative models for topological signal generation and matching. This returns to other models for topological signals based on score matching or flow matching.
  • Exploit the model applications in biological data such as brain signals and single-cell data, as well as seismic signals and ocean currents.
    •
    Demo 1: Transporting rotational ocean currents to rotational-free ones.
    Demo 2: Bridging active and resting brain fMRI signals.
    Demo 3: Trajectory inference of single-cell data. From left to right: groundtruth, predicted-tsb, and predicted-sb.
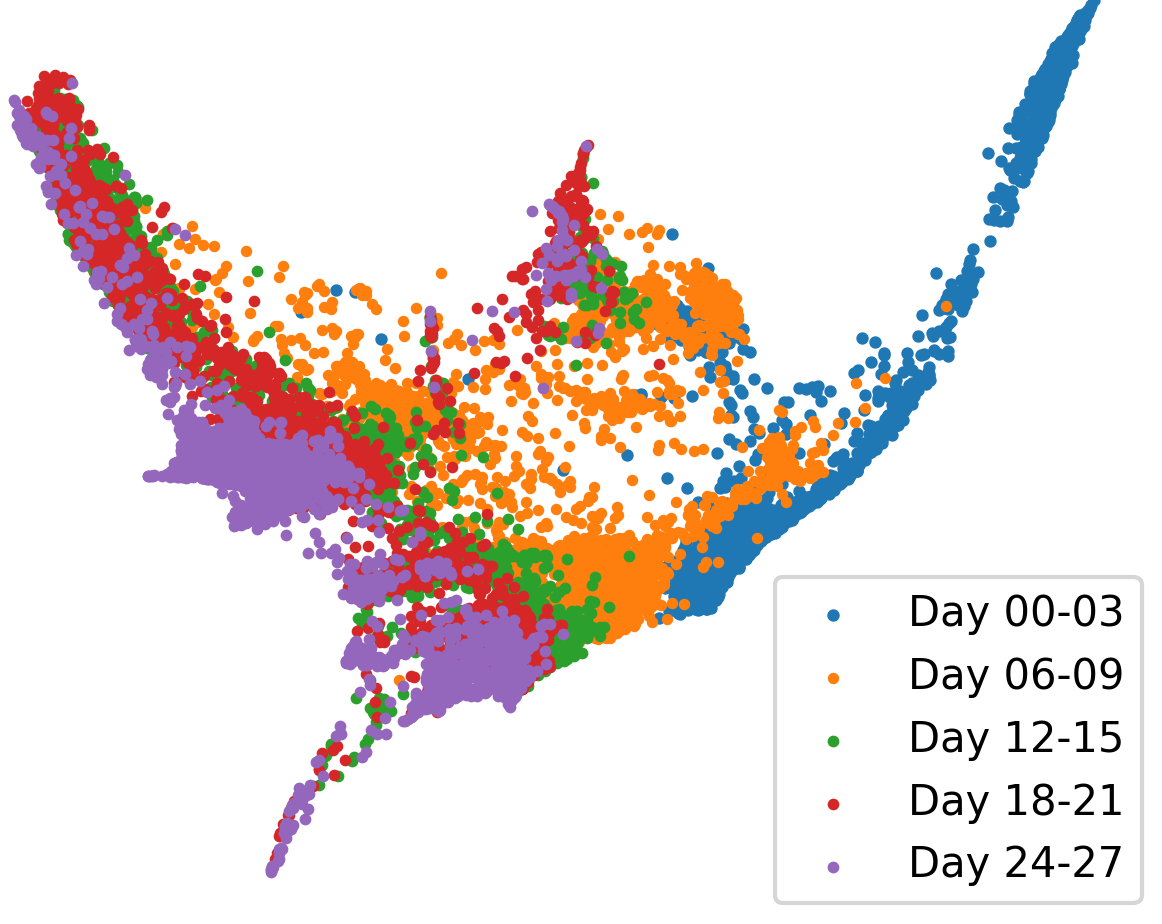
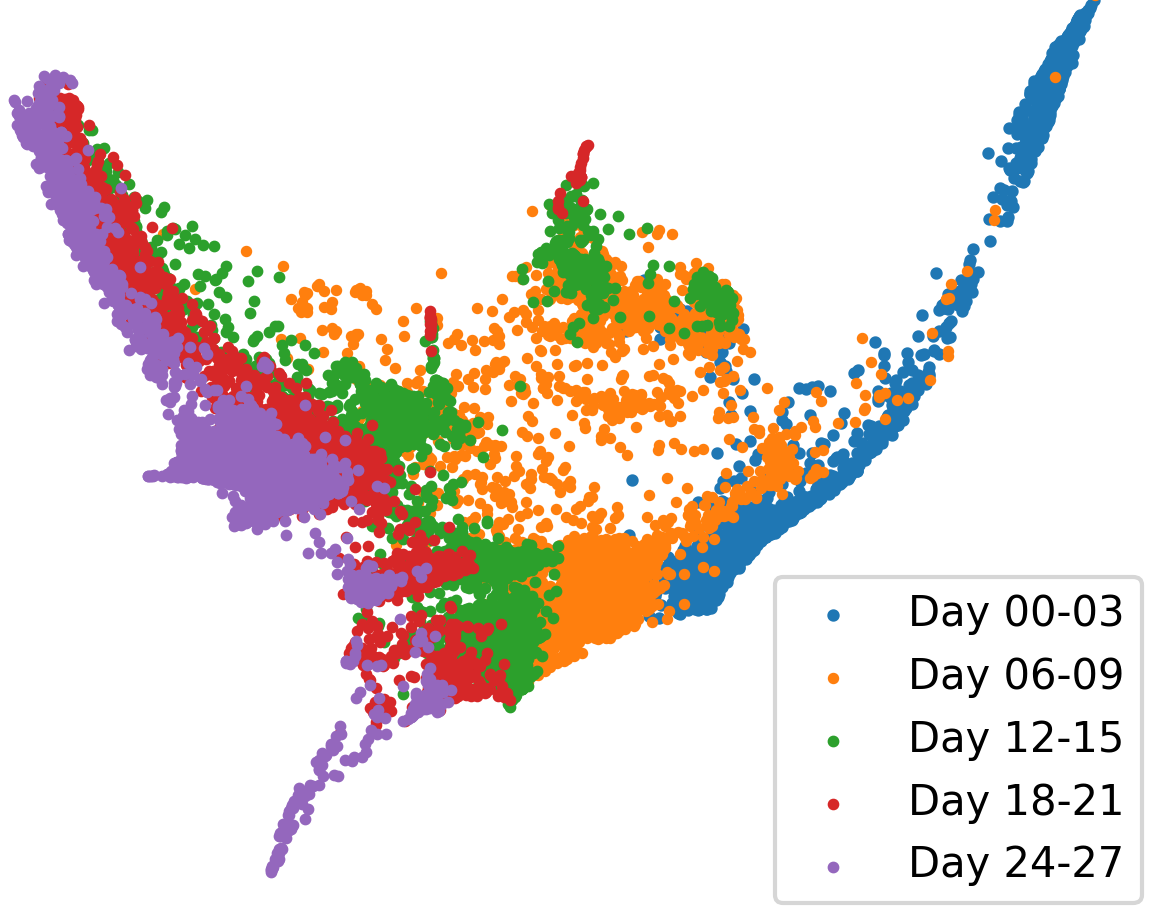
    Hodge-compositional Edge Gaussian Processes
    Maosheng Yang, Viacheslav Borovitskiy, Elvin Isufi
    AISTATS, 2024
    [paper] [code] [slides] (model integrated in Geometric Kernels library)
  • Built principled diffusion and Matérn Gaussian processes on simplicial complexes based on combinatorial Hodge theory, based on stochastic differential equations on the edge space. For example, see the diffusion process on nodes and edges starting from one node or edge as follows.
  • This allows for statistical modeling of edge flows with various properties like being divergence-free or curl-free.
  • Applications in: arbitrary-free forex interpolation, ocean current modeling, and state estimation in water networks.
    •
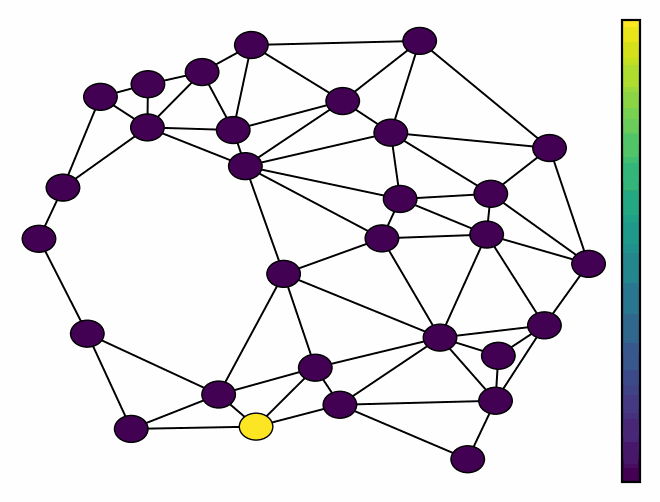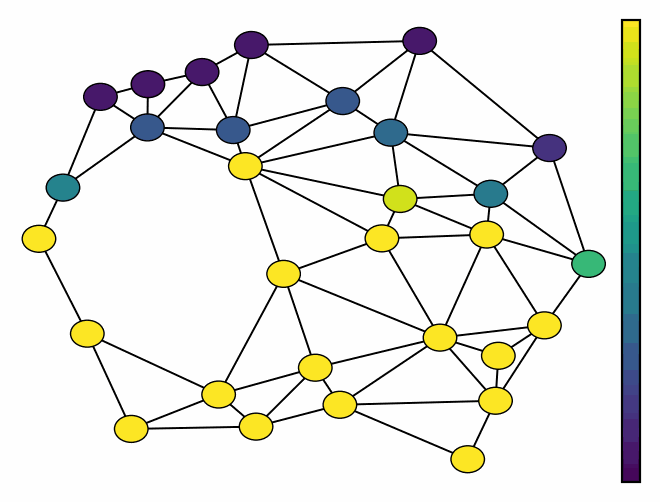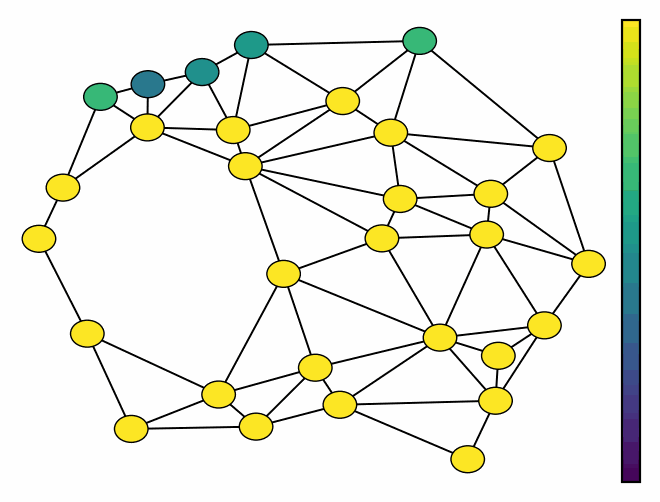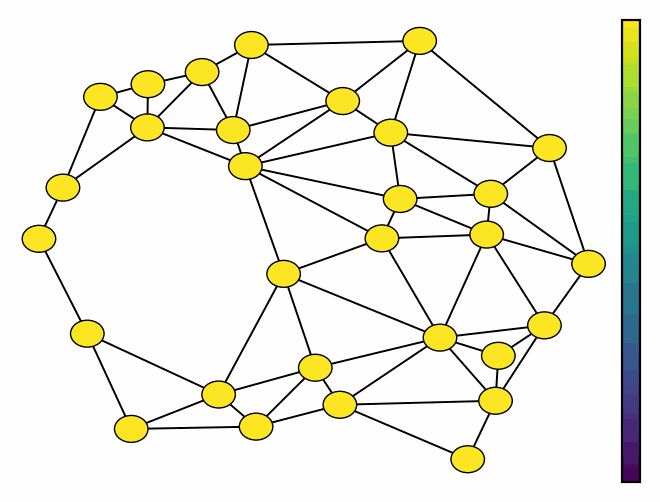
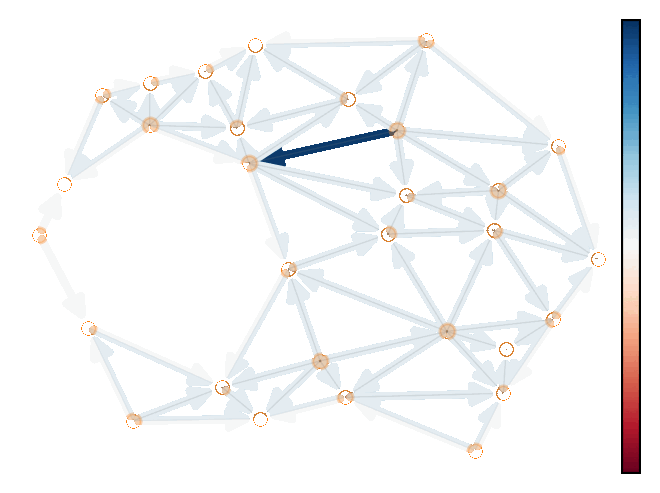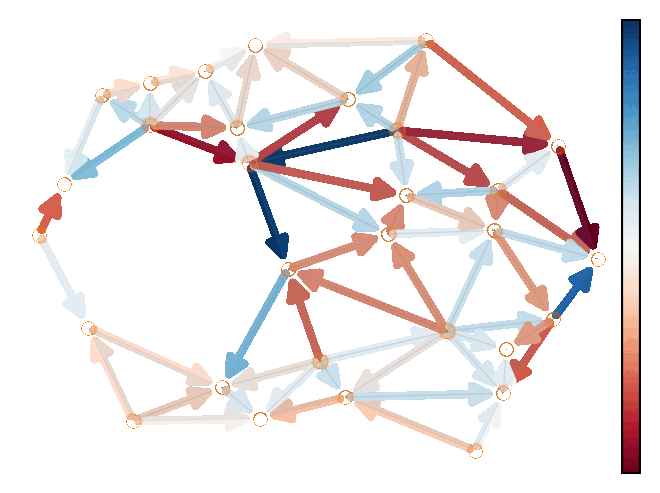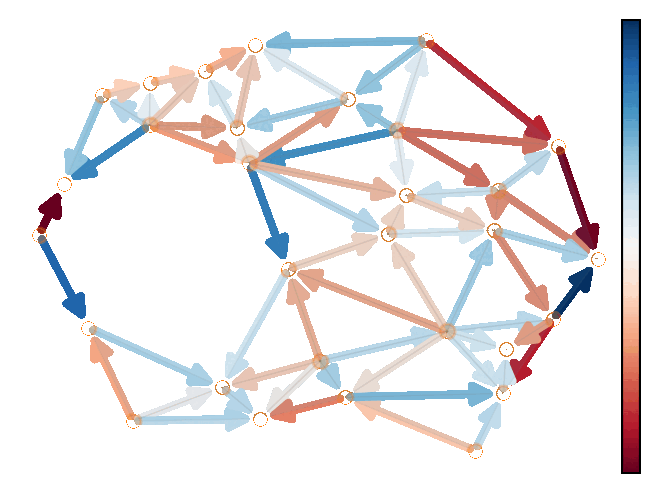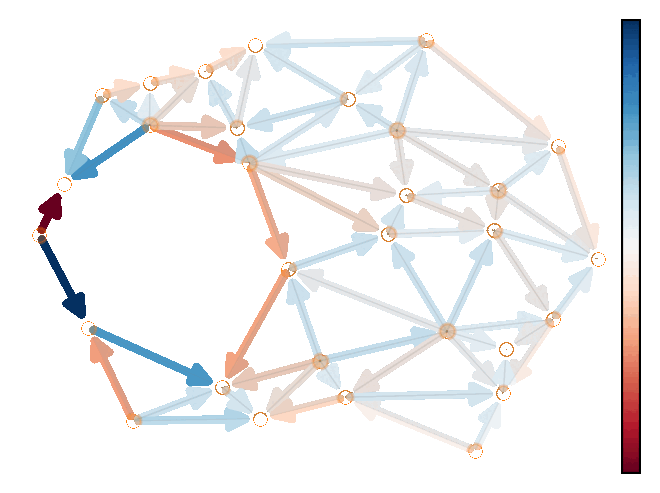
    Demo 1: Modeling the solenodial and irrotational ocean current velocity field.
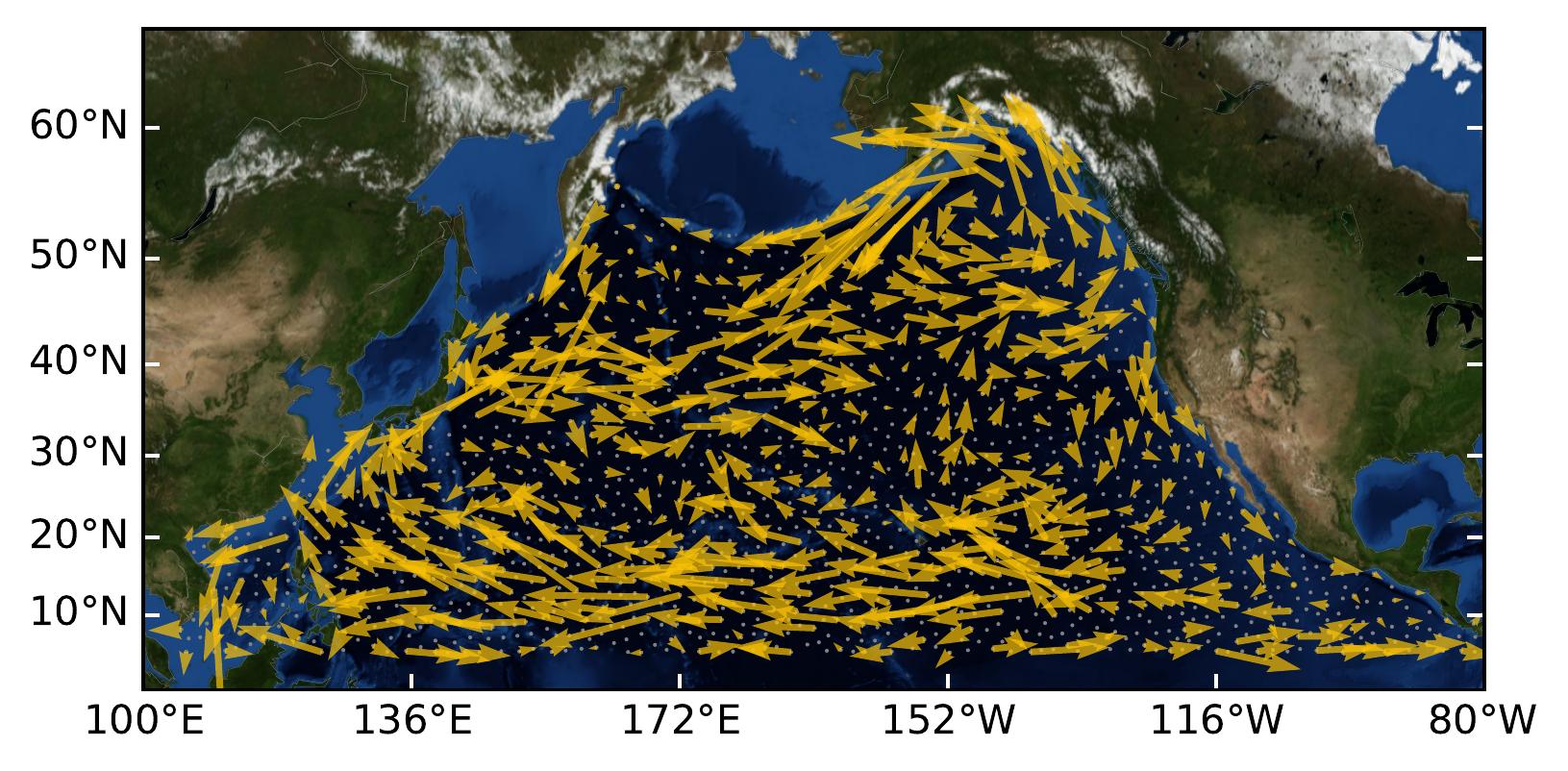
    Posterior Vector Field Gradient Vector Field Curl Vector Field
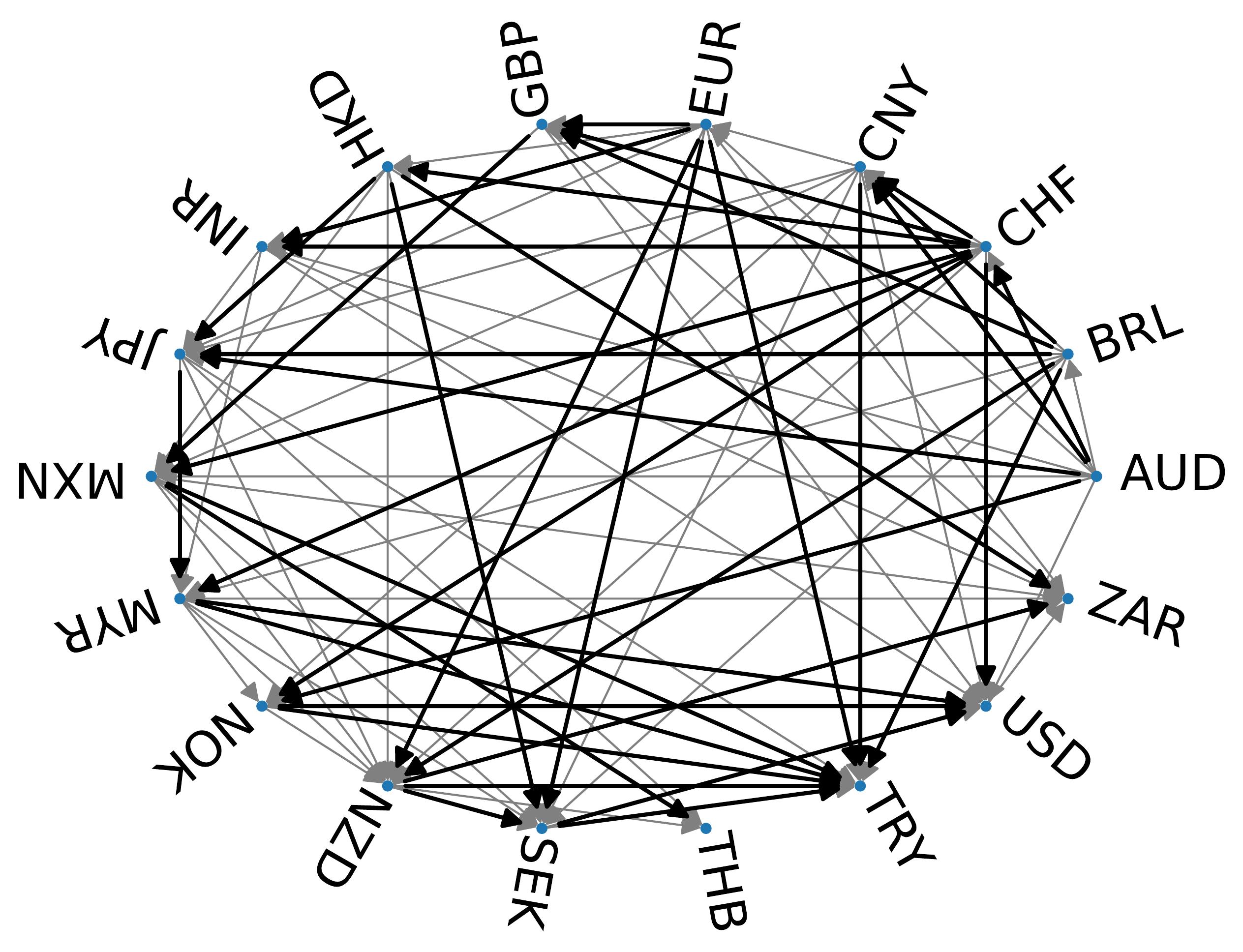
    Demo 2: Interpolating arbitrage-free foreign currency exchange.
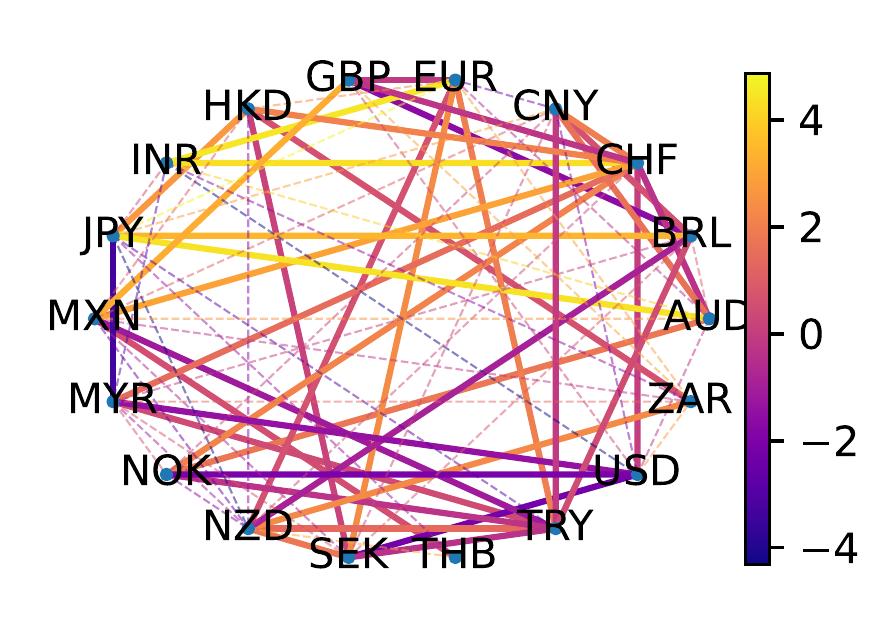
    Hodge-Aware Learning on Simplicial Complexes
    Maosheng Yang, Elvin Isufi
    [paper] [code] (model integrated in TopoModelX for topological deep learning)
    arXiv, 2023
  • Proposed a general convolutional learning framework for data in simplicial complexes, including node data, edge flows, triangle data, and more.
  • The framework incorporates theoretical analysis of locality, symmetry, spectral properties based on Hodge decomposition, and stability analysis.
  • Applications include foreign currency exchange, triangle and tetrahedron (higher-order link) predictions, and trajectory prediction for ocean buoys.
    • Simplicial Convolutional Neural Networks
    Maosheng Yang, Elvin Isufi, Geert Leus
    [paper] [code] (model integrated in TopoModelX for topological deep learning)
    ICASSP, 2022
  • Designed a neural network based on simplicial convolutional filters for learning from data on simplices of one certain order, e.g., edge flows, which returns to graph convolutional neural networks for node data.
    • Simplicial Convolutional Filters
    Maosheng Yang, Elvin Isufi, Michael T. Schaub, and Geert Leus
    IEEE Transactions on Signal Processing, 2022
  • Proposed spectral methods for signals defined on simplicial complexes, based on discrete calculus.
  • Built the convolutional filters for simplicial complexes based on the Hodge decomposition.
  • Large-scale filter implementation based on Chebyshev polynomials on simplicial complexes.
  • Generalized Graph signal processing framework to simplicial complexes.
    • [paper] [code]

    Talks

    This is a recently updated material on my PhD work Understanding and Learning Simplicial Signals (slides for personal use) that I used for some talks. I appreciate the opportunity to present my work in the other research groups, workshops and conferences.

    Teaching

    Teaching Assistant
    BSc & MSc Project Supervision
    • Three projects involving 15 computer science bachelor students on topics: recommender systems, deep neural networks and graph neural networks Apr - Jul 2022, 2023, 2024
    • Two master projects on topics: topological unrolling networks and building a Python library for topological signal processing Sep 2022 - Apr 2023, Jan - Aug 2024
      •

    Open Source Projects

    • Participation in the Python module TopoModelX for topological deep learning (check the related overview paper 1 and paper 2), where I implemented two models (SCNN, SCCNN) that we proposed for convolutional learning on simplicial complexes.
    • Participation in the Python module GeometricKernels. It implements kernels including the heat and Matérn classes on non-Euclidean spaces such as Riemannian manifolds, graphs and meshes, where I implemented kernels on the edge space of graphs or simplicial complexes.

    Service

    Conference Reviewer: ICASSP, EUSIPCO, ICML, NeurIPS, ICLR
    Journal Reviewer: IEEE TSP, IEEE TSIPN, IEEE SPL, IEEE TNNLS